Física - Resistores - Interessante
4 participantes
Página 1 de 1
 Física - Resistores - Interessante
Física - Resistores - Interessante
Determine a resistência equivalente entre os pontos A e C' do trecho de circuito abaixo.

Gabarito:
(Só vejam se já tiverem resolvido o problema !!! Basta clicar em "Spoiler")

Gabarito:
(Só vejam se já tiverem resolvido o problema !!! Basta clicar em "Spoiler")
- Spoiler:
 Re: Física - Resistores - Interessante
Re: Física - Resistores - Interessante
https://2img.net/r/ihimg/photo/my-images/713/0510112329.jpg/
Simplifiquei bastante , pra mim o circuito resta agora calcular tudo isso.
Fiz uma álgebra meio loca que não deu certo.
Acho que agora o problema eh conta.
Simplifiquei bastante , pra mim o circuito resta agora calcular tudo isso.
Fiz uma álgebra meio loca que não deu certo.
Acho que agora o problema eh conta.
gabrieldpb- Mensagens : 22
Data de inscrição : 04/09/2011
 Re: Física - Resistores - Interessante
Re: Física - Resistores - Interessante
hahah finalmente em luis a resolução
muito dificil, mas uma ótima resolução
muito dificil, mas uma ótima resolução
gabrieldpb- Mensagens : 22
Data de inscrição : 04/09/2011
 Re: Física - Resistores - Interessante
Re: Física - Resistores - Interessante
De fato, é uma questão muito interessante. Acho que eu poderia ficar tentando essa questão que não teria a mesma ideia para resolver.

marcos- Mensagens : 28
Data de inscrição : 03/09/2011
 Re: Física - Resistores - Interessante
Re: Física - Resistores - Interessante
Seja 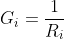 , para i = 1,2,3. Isto são os nós do circuito, a soma dos nós temos:
, para i = 1,2,3. Isto são os nós do circuito, a soma dos nós temos: 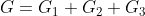
Para ficar um pouco claro, vamos indexar cada nó do cubo, como segue:
começando pelo A com 0,1,2,3 no sentido anti-horário. Agora os 4 nós de cima, 5,6,7 no sentido horário, tal que o nó 4 está acima do 3º nó, no vértice do cubo. Aterrando o nó 0 (GND) e plugando uma fonte V no cirucito, temos em função de C' (5º nó). Assim chegaremos a equação do nó para termos a Req entre A e C'.
\cdot&space;\left(&space;\begin{matrix}&space;{{v}_{1}}&space;\\&space;{{v}_{2}}&space;\\&space;{{v}_{3}}&space;\\&space;{{v}_{4}}&space;\\&space;{{v}_{5}}&space;\\&space;{{v}_{6}}&space;\\&space;{{v}_{7}}&space;\\&space;-I&space;\\&space;\end{matrix}&space;\right)=\left(&space;\begin{matrix}&space;0&space;\\&space;0&space;\\&space;0&space;\\&space;0&space;\\&space;0&space;\\&space;0&space;\\&space;0&space;\\&space;V&space;\\&space;\end{matrix}&space;\right))
Para obter Req entre os nós 0(A) e 5(C'), calcular a corrente I, pela regra de Cramer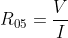
Calculando esse determinante monstro, chegaremos ao Req do circuito, mas isso dá muito trabalho.
PS: Para entender bem a resolução, leiam este artigo: http://www.4shared.com/document/wOm3_vjt/HOW_TO_SOLVE_CIRCUITS_WITH_DET.html?
Para ficar um pouco claro, vamos indexar cada nó do cubo, como segue:
começando pelo A com 0,1,2,3 no sentido anti-horário. Agora os 4 nós de cima, 5,6,7 no sentido horário, tal que o nó 4 está acima do 3º nó, no vértice do cubo. Aterrando o nó 0 (GND) e plugando uma fonte V no cirucito, temos em função de C' (5º nó). Assim chegaremos a equação do nó para termos a Req entre A e C'.
Para obter Req entre os nós 0(A) e 5(C'), calcular a corrente I, pela regra de Cramer
Calculando esse determinante monstro, chegaremos ao Req do circuito, mas isso dá muito trabalho.
PS: Para entender bem a resolução, leiam este artigo: http://www.4shared.com/document/wOm3_vjt/HOW_TO_SOLVE_CIRCUITS_WITH_DET.html?
Última edição por Luís Eduardo em Sáb Out 22, 2011 6:06 pm, editado 2 vez(es) (Motivo da edição : Códigos LaTeX sem funcionar)
Kenne- Mensagens : 19
Data de inscrição : 16/10/2011
 Re: Física - Resistores - Interessante
Re: Física - Resistores - Interessante
Kenne,
Isso seria uma outra forma de resolver, mas não sei se é a mais prática kkk.
Não entendi muito bem sua resolução.
OBS: Perceba que editei sua mensagem já que estava com problemas para aparecer os códigos LaTeX.
Isso seria uma outra forma de resolver, mas não sei se é a mais prática kkk.
Não entendi muito bem sua resolução.
OBS: Perceba que editei sua mensagem já que estava com problemas para aparecer os códigos LaTeX.
 Re: Física - Resistores - Interessante
Re: Física - Resistores - Interessante
Então Luís, basta ver que eu utilizei o artificio de indexação dos nos do circuito, tomando cada ponto do nó como parte literal. Se você seguir cada passo, você vai ver que temos a fonte V e claro, uma corrente I circulando pelo cirucito. Cada parte do mesmo, passa uma determinada tensão e corrente e, cada uma delas nos fornecerá a resistencia que no final sera a equivalente. A razão disso, será o determinante que pode ser calculado pela regra de Cramer. Vou tentar ser mais didatico.
Kenne- Mensagens : 19
Data de inscrição : 16/10/2011
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|





