CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
3 participantes
Página 1 de 1
 CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
DUAS CARGAS IDÊNTICAS SÃO COLOCADAS A UMA DISTÂNCIA L UMA DA OUTRA E SÃO DEIXADAS LIVRES. APÓS UM TEMPO T A DISTÂNCIA ENTRE AS CARGAS DUPLICOU. ESTAS MESMAS CARGAS SÃO COLOCADAS A UMA DISTÂNCIA 2L E SÃO DEIXADAS LIVRES. DETERMINE O TEMPO PARA O QUAL A DISTÂNCIA ENTRE AS CARGAS DUPLICOU.
Gabarito:
Gabarito:
- Spoiler:
MARCOS HAROLDO DANTAS- Mensagens : 8
Data de inscrição : 09/09/2011
 Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Situação I)
(+) |-------------------| (+)
....................L..............
Força elétrica = Fe = k.q²/L²
Força resultante = F = m.a
=> a = k.q²/m.L² (aceleração de cada bolinha)
A aceleração relativa entre as bolinhas é ar = 2.a = 2. k.q²/m.L²
Sabe-se que: S = a.t²/2=> T² = m.L³/k.q² (i)
Situação II)
(+) |--------------------------------------| (+)
......................................2L..............
Fe' = k.q²/(2L)² => Fe' = kq²/4L² => a' = kq²/4mL²
A aceleração relativa entre as bolinhas é:
ar' = 2.a' => ar' = 2.k.q²/4.m.L² => ar' = kq²/2.m.L²
Sabe-se que: S = a.t²/2 => 2L = k.q².t²/2.2.m.L²
=> t² = 8.L³.m/k.q² => de I => t² = 8T² => t = V8.T
(+) |-------------------| (+)
....................L..............
Força elétrica = Fe = k.q²/L²
Força resultante = F = m.a
=> a = k.q²/m.L² (aceleração de cada bolinha)
A aceleração relativa entre as bolinhas é ar = 2.a = 2. k.q²/m.L²
Sabe-se que: S = a.t²/2=> T² = m.L³/k.q² (i)
Situação II)
(+) |--------------------------------------| (+)
......................................2L..............
Fe' = k.q²/(2L)² => Fe' = kq²/4L² => a' = kq²/4mL²
A aceleração relativa entre as bolinhas é:
ar' = 2.a' => ar' = 2.k.q²/4.m.L² => ar' = kq²/2.m.L²
Sabe-se que: S = a.t²/2 => 2L = k.q².t²/2.2.m.L²
=> t² = 8.L³.m/k.q² => de I => t² = 8T² => t = V8.T
 Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Luis, mas a aceleração vai variar com a distância entre as cargas...Acho q n pode dizer q S=at²/2 e q, inclusive, o problema da questão está em a aceleração n ser constante...

Lucas da Cruz- Mensagens : 150
Data de inscrição : 04/09/2011
Idade : 29
Localização : Fortaleza-CE
 Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Eu pensei em espelhar o movimento das cargas (espelho no meio da reta q contém as duas cargas) , assim, o movimento das imagens seria de atração, o q nos permitiria trabalhar com uma elipse degenerada semelhante à usada naqueles problemas de gravitação...
Aí ficaria que uma das cargas estaria num foco da elipse e a outra seria movimentada com o dobro da aceleração...
A "área" percorrida pela carga em movimento seria(1ª situação) :
S=(1/4)pi.a.b +bc/2 e=c/a--> c=ea
S= (1/4).pi.ab +e.a.b/2
E a área total seria: St=piab
O período total seria dado por : P=2pi sqrt[L/(2KQ²/ML²)]
E a relação entre ele e o tempo para as cargas se encontrarem seria a mesma que a relação entre a área total e a área percorrida da elipse:
T/P=S/St <=> T/P=1/4 +1/2pi , já que a elipse é degenerada e-->1
Logo, chamando 1/4+1/2pi =K, temos que : T=P.K
Mas, para a segunda situação , temos que P'=2pisqrt[2L/(2KQ²/4ML²)], ou seja, P'=Psqrt8 .
Assim, analogamente ao primeiro caso, temos tb que: T'=P'K.
Substituindo Psqrt8=P' e dividindo T' por T, obtemos:
T'/T=P'K/PK<=>T'/T=K.Psqrt8/K.P<=> T'=Tsqrt8
Aí ficaria que uma das cargas estaria num foco da elipse e a outra seria movimentada com o dobro da aceleração...
A "área" percorrida pela carga em movimento seria(1ª situação) :
S=(1/4)pi.a.b +bc/2 e=c/a--> c=ea
S= (1/4).pi.ab +e.a.b/2
E a área total seria: St=piab
O período total seria dado por : P=2pi sqrt[L/(2KQ²/ML²)]
E a relação entre ele e o tempo para as cargas se encontrarem seria a mesma que a relação entre a área total e a área percorrida da elipse:
T/P=S/St <=> T/P=1/4 +1/2pi , já que a elipse é degenerada e-->1
Logo, chamando 1/4+1/2pi =K, temos que : T=P.K
Mas, para a segunda situação , temos que P'=2pisqrt[2L/(2KQ²/4ML²)], ou seja, P'=Psqrt8 .
Assim, analogamente ao primeiro caso, temos tb que: T'=P'K.
Substituindo Psqrt8=P' e dividindo T' por T, obtemos:
T'/T=P'K/PK<=>T'/T=K.Psqrt8/K.P<=> T'=Tsqrt8

Lucas da Cruz- Mensagens : 150
Data de inscrição : 04/09/2011
Idade : 29
Localização : Fortaleza-CE
 Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Re: CARGAS EM MOVIMENTO- CÁLCULO DE TEMPO
Resolução
Para resolver este problema, iremos utilizar o teorema do valor médio como provaremos a seguir.
O gráfico da aceleração em função do tempo será similar à figura abaixo:

Pelo gráfico, sabemos que:
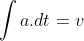
Mas, queremos provar que: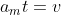
Para isso, devemos aplicar o teorema do valor médio:
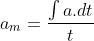
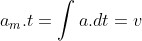
Agora, para resolver o problema basta utilizarmos a aceleração média.
Primeiro caso:

As duas cargas estão a uma distância L uma da outra e após um tempo T a distância entre elas duplicou.
Então, sabemos pelo teorema do valor médio que:
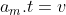 (I)
(I)
Pela conservação da energia mecânica temos que:
)
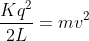
Como temos a aceleração média podemos usar a equação de Torricelli:
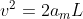 (II)
(II)
Elevando a equação (I) ao quadrado e igualando com a equação (II) achamos que:
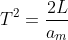 (III)
(III)
Segundo caso:
Agora iremos analisar o segundo caso quando as cargas estão dispostas a uma distância de 2L e depois de um tempo t' essa distância dobra.

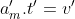 (IV)
(IV)
Usando a conservação da energia mecânica:
^2)
Isolando o (v')²:
^2=\frac{1}{2}\left&space;(\frac{Kq^2}{2mL}&space;\right&space;))
Note que: v² = Kq²/2mL, então:
^2=\frac{v^2}{2})
Usando torricelli:
^2=2.a'_{m}.2L=4.a'_{m}.L) (V)
(V)
Elevando ao quadrado a equação (IV) e igualando a equação (V) iremos encontrar que:
^2&space;=&space;\frac{4L}{a'_{m}})
Agora, basta encontrar uma relação entre a'm e am e assim encontraremos a resposta para o problema. Para isso, sabemos que:
^2&space;=&space;v^2&space;\\&space;\\&space;8.a'_{m}.L=2.a_{m}.L\\&space;\\&space;4.a'_{m}=a_{m})
Sabendo disso, o problema terminou já que:
^2&space;=&space;\frac{4L}{\frac{a_{m}}{4}}=\frac{16L}{a_{m}}=8.T^2)
Então,
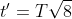
Para resolver este problema, iremos utilizar o teorema do valor médio como provaremos a seguir.
O gráfico da aceleração em função do tempo será similar à figura abaixo:

Pelo gráfico, sabemos que:
Mas, queremos provar que:
Para isso, devemos aplicar o teorema do valor médio:
Agora, para resolver o problema basta utilizarmos a aceleração média.
Primeiro caso:

As duas cargas estão a uma distância L uma da outra e após um tempo T a distância entre elas duplicou.
Então, sabemos pelo teorema do valor médio que:
Pela conservação da energia mecânica temos que:
Como temos a aceleração média podemos usar a equação de Torricelli:
Elevando a equação (I) ao quadrado e igualando com a equação (II) achamos que:
Segundo caso:
Agora iremos analisar o segundo caso quando as cargas estão dispostas a uma distância de 2L e depois de um tempo t' essa distância dobra.

Usando a conservação da energia mecânica:
Isolando o (v')²:
Note que: v² = Kq²/2mL, então:
Usando torricelli:
Elevando ao quadrado a equação (IV) e igualando a equação (V) iremos encontrar que:
Agora, basta encontrar uma relação entre a'm e am e assim encontraremos a resposta para o problema. Para isso, sabemos que:
Sabendo disso, o problema terminou já que:
Então,
 Tópicos semelhantes
Tópicos semelhantes» Movimento harmonico
» Quantidade de Movimento - Projétil
» (IPhO-67) Lançamento e Quantidade de Movimento
» Quantidade de Movimento - Projétil
» (IPhO-67) Lançamento e Quantidade de Movimento
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos

